Home Sensing Primer Glossary Physics Related Technologies Acknowledgements
Continuum spectra
A prism can be used to intercept a beam of sunlight and transform it into a fan of colors, where the colors are sorted by wavelength. This pretty display of colors is called a spectrum. Spectra are filled with information, and studying them is key to all of remote sensing, as well as much of chemistry, physics, and nearly all of astronomy. The reason spectra are so important is that the precise nature of a spectrum can be used to deduce things about the entity that produced the light and the events that happened to the beam as it traveled to your instrumentation. In this section, we will talk about what and why these things can be inferred.
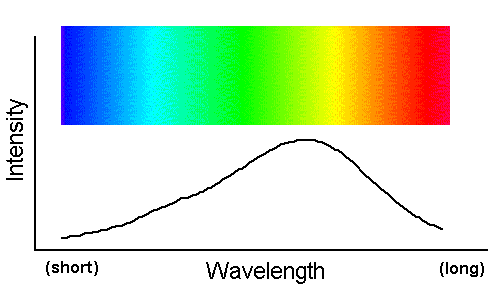
A beam of light that contains a broad, smooth distribution of photon wavelengths is called a "continuum spectrum."
This spectrum is familiar as the broad wash of colors in a rainbow. The figure above graphs intensity (the number of photons at each
wavelength) vs. wavelength
for a hypothetical continuum spectrum. Notice the line is smooth and continuous--hence the name, continuum spectrum. The rainbow-like bar of
color shows how the visible portion of such a spectrum appears.
Continuum spectra are produced by the thermal energy of the radiating source. Since everything in the universe has at least
some energy, everything produces a continuum spectrum. The sun, being very hot, produces its continuum spectrum mostly in the visible part
of the spectrum. Humans are about 20 times cooler than the sun, so the continuum radiation emitted by their skin is much less
energetic--military designers of heat-seeking missiles know that their instruments must home in on objects producing continuum radiation at
infrared wavelengths (i.e. low energies). Extremely hot objects like supermassive stars produce most of their energy in ultraviolet
wavelengths.
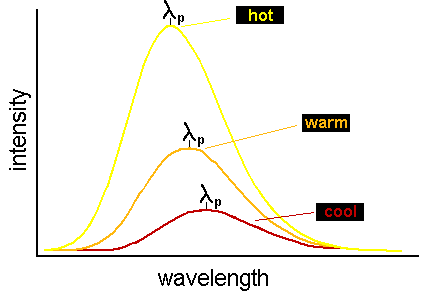
The fact that hotter objects produce continuum spectra that peak (i.e. have maximum energy output) at shorter wavelengths is
formalized by Wien's Law, named after Wilhelm Wien:
pT=constant,where T is the temperature in Kelvins, and p
is the wavelength corresponding to the intensity peak in the continuum spectrum. Note that
hotter objects (i.e. ones with a greater temperature T) have continuum spectra that peak at smaller (shorter) wavelengths. This is
graphically represented in the figure below:
Another useful equation regarding continuum spectra is Stephan-Boltzmann's Law, which says (among other things) that the total power radiated by an object (combined over all wavelengths) is:
T4. For those who have forgotten their mathematical symbols, this equation means that the total power P radiated by an object
is proportional to the temperature raised to the fourth power: hotter objects radiate a great deal more energy than cooler objects. (Notice
that in the figure above, the area under the curve for the hottest spectrum is larger than for the cooler spectra.) Wien's Law and
Stephan-Boltzmann's Law are of particular relevance to those doing remote sensing at infrared wavelengths. Hot surfaces
like sun-heated roads and rocks are much brighter at infrared wavelengths than are surfaces like cold bodies of water.
 |
 |